自由能方法及应用（三）炼金术自由能计算方法在药物发现中的历史

理论基础

尽管自由能微扰（FEP）方法直到1980年代才引起计算机辅助药物设计（CADD）领域的关注，其理论基础还要回溯到1930年代的Peierls的工作，随后在对非极性气体的性质进行理论探索时，Zwanzig推导了FEP的主方程（参见等式1）：

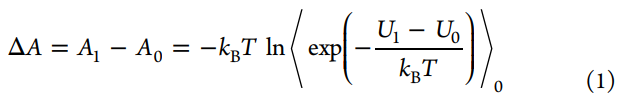
FEP方程的内在美在于它可以通过对状态0的势能引导的配置进行采样然后计算采样配置中两个状态的势能，从而计算两个系综状态（状态0和状态1）之间的自由能差。在等式1中，⟨⟩0代表在状态0下的玻尔兹曼平均值，T是温度，kB是玻尔兹曼常数，U1和U0分别是状态1和状态0的势能。在这里，我们使用亥姆霍兹（Helmholtz）自由能差（ΔA）代替吉布斯（Gibbs）自由能差（ΔG），但是在ΔPV值通常较小的凝聚相模拟中，两者的差异可忽略不计。从表面上看，使用该主方程似乎很简单，但FEP计算的收敛性并不容易实现，尤其是对于两个端态集合的平衡分布几乎没有重叠的体系。Kirkwood在1935年描述的使用耦合参数的想法极大地有利于FEP计算。简而言之，就是经由耦合参数λ引入一系列中间状态。随着λ从0递增到1，中间状态的势能（Uλ）从U0变为U1。然后计算相邻状态之间的ΔAs，所有ΔAs的总和得出总ΔA。用于将中间状态定义为λ函数的电势函数的典型形式是参考状态U0的电势与U1的电势的线性组合（参见等式2）。 

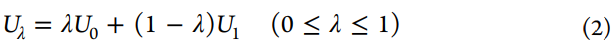
另一种有效估计自由能差的方法是Bennett在1976年开发的Bennett acceptance ratio（BAR），通过类比FEP方程，Bennett推导出了等式3，其中引入了加权函数（w）。 

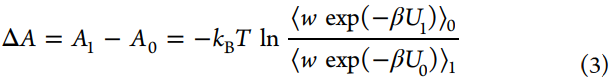
通过最小化自由能差的期望平方误差，Bennett获得了方程4的最佳加权函数，进而可以通过对ΔA进行迭代试验来求解。

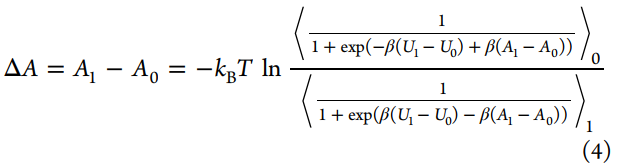
与Zwanzig的方程式不同，BAR分析需要在两种状态下进行采样配置。2008年，多状态的BAR（MBAR）方法得到了报道，该方法通过组合来自多个状态而不是仅来自两个状态的模拟数据来估算自由能。另一种常规方法，即热力学积分（TI），是基于Kirkwood在液体理论方面的工作得出的，其通过对状态λ相对于λ的玻尔兹曼平均势能导数进行积分来计算ΔA（参见等式5）。

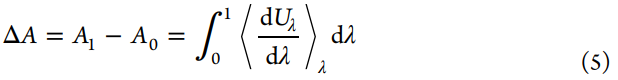
技术支持

为了进行炼金术自由能（AFE）计算，基于上述理论基础，我们需要生成代表性结构并评估相应的势能。因此，模拟仿真技术和力场的发展成为AFEM计算的关键因素。一种主要的采样技术是蒙特卡洛（MC）模拟。简而言之，MC模拟从给定的配置开始，然后以最终采样的配置恢复实际整体的真实分布的方式接受或拒绝下一个建议的配置。另一种主要的采样技术是分子动力学（MD）模拟。MD模拟涉及沿时间轴的采样配置。1964年，Rahman在液态氩方面发表了具有里程碑意义的MD模拟工作，并首次使用了Lennard-Jones势描述了氩原子。随着适用于生物分子的力场的发展，1977年，McCammon，Gelin和Karplus在Levitt和Warshel的Lifson实验室开发的模拟程序的基础上，首次对蛋白质进行了MD模拟。同一年Berendsen开发了“SHAKE”算法，该算法约束了高频重原子形成的氢键，这一贡献使得在可用计算机资源允许的情况下将MD模拟中使用的时间步长增大2倍来进行更加充分的采样成为可能。此外，维持温度恒定和压力恒定的算法的实现使MD模拟能够采样物理上实际的配置。生物分子力场的发展是基于Lifson实验室在1960年代后期所做的开创性工作发展而来，势能函数的形式参见公式6。其中前三项分别表示键长、键角和二面角对势能的贡献，后两项分别表示非键相互作用的范德华相互作用和成对静电相互作用。在1980年代，基于Lifson力场模型开发了其他早期力场和程序，包括Karplus等人开发的CHARMM、Kollman等人开发的AMBER、Jorgensen等人开发的OPLS以及Berendsen和van Gunsteren等人开发的GROMOS。

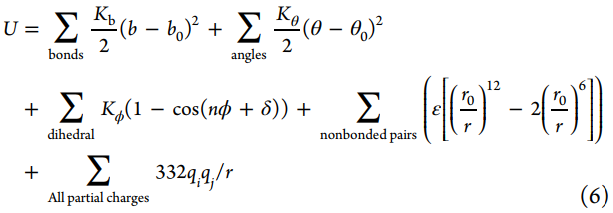
进行AFE计算的另一项重要的技术支持是开发强大而准确的水模型。药物分子的绝对结合自由能和相对结合自由能都受溶剂影响。因此，精确建模描述水和小分子的溶剂化至关重要。隐性水模型，如Poisson–Boltzmann或Generalized Born模型，可用于模拟溶剂对药物结合的影响，但是许多水分子结合相关受体或水分子-药物相互作用是特定的，因此需要使用显式的水分子模型以获得更高质量的结果。例如，活性位点处的水分子的置换在自由能预测中可以发挥显著作用。根据使用了多少个额外的虚拟带电原子（即没有vdW势项），水模型可以分为三点、四点、五点和六点模型。Jorgensen是开发用于分子模拟的实用而精确的水模型的先驱。他开发了TIP（transferable intermolecular potentials）模型来创建用于水、酒精和乙醚模拟的溶剂模型，并在此基础上创建了TIPS2，TIP3P和TIP4P水模型，然后将这些水模型与一系列实验结构和热力学性质进行了比较，这些性质为将来对水模型进行评估奠定了基础。同样在1981年，Berendsen和他的同事们设计了SPC（simple point charge）水模型，并通过自我能量校正改进了SPC模型，创建了SPC/E水模型。目前TIP3P和SPC/E水模型得到了最广泛的应用。尽管如此，开发更精确的水模型仍然是一个充满挑战的研究领域。

AFE早期研究

Postma、Berendsen和Haak在1982年报道了关于在水中形成空腔的FEP计算。这项工作几年后，Jorgensen和Ravimohan于1985年计算了稀溶液中甲醇和乙烷的相对水合自由能，其结果与实验基本吻合。这预示着FEP计算在CADD中的潜力，因为相对溶剂化自由能在确定一个共同受体位点上两个配体的相对结合自由能方面起着主要作用。除了将FEP应用于相对水合自由能计算外，Jorgensen及其同事还应用FEP为SN1反应（（CH3）3CCl的解离）建立了平均力势（PMF）分布，从而开启了溶剂化对反应过程影响的研究方向。Jorgensen的工作鼓舞了Kollman及其同事将FEP应用于其AMBER MD模拟程序，并且他们运用FEP/MD方法研究了包括有机分子和蛋白质抑制剂体系在内的各种系统。这些早期研究显示了AFEM在不同体系上的应用潜力，但使AFEM广泛应用于CADD的主要推动力是实现了热力学循环的吉布斯或亥姆霍兹自由能等状态函数的幂运算，从而简化了相对结合自由能（RBFE）计算的计算。图1所示的上下部过程分别表示配体L1和配体L2与受体位点R的绝对结合自由能（ABFE）。通过连接图1的上部和下部过程，我们发现ΔΔA=ΔA1–ΔA2可以通过两个垂直过程表示的炼金术转化获得ΔΔA=ΔA3–ΔA4。因此，两个配体的RBFE可以通过以下两个炼金术过程的AFE计算获得：R + L1→R + L2和RL1→RL2。以这种方式转换问题会将两个计算量大的计算转换为两个计算量大的AFE计算。除了使这些计算更容易处理之外，热力学循环概念还提供了误差消除功能，从而提高了计算出的自由能的精度。

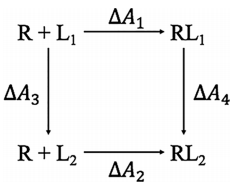
图1 热力学循环：R是受体，L1和L2是两个不同的配体，RL1代表与R结合的L1，RL2代表与R结合的L2。

图片源自JCIM.

AFE在CADD中的现代研究

CADD中的第一个现代AFE研究是Wong和McCammon关于“酶和抑制剂的动力学与设计”的研究，并首次证明了“热力学循环扰动法”在CADD中的适用性。1986年，通过在AMBER程序中实施的FEP方法，Kollman及其同事研究了一对与嗜热菌素结合的抑制剂（即膦酰胺和膦酸酯），计算得出的ΔΔA值为4.21±0.54 kcal/mol，与4.10 kcal/mol的实验值非常接近。此外，在McCammon和科尔曼Kollman组的两项研究中，抑制剂的相对溶剂化自由能对计算出的ΔΔA做出了重要贡献，这进一步说明了准确描述有机分子与水分子之间相互作用的重要性。随后，Kollman及其同事将研究扩展到除了配体结合之外，还进行了位点特异性诱变对酶催化的影响。经过1980年代的初步研究后，CADD中的AFE研究在1990年代得到了进一步的发展，但是尽管MC模拟在宿主-客体系统的早期FEP研究和相对溶剂自由能的计算中是成功的，由于围绕采样效率的问题，其在蛋白质模拟中的使用受到限制。在一个蛋白质区域中，一个小幅度的主链角度的变化可能会导致远端部位大幅度的移动，因此，总体接受率将很小。Jorgensen于1997年在CADD中进行了前两次现代MC/FEP研究与实验取得了很好的一致性，但两项研究均使蛋白质主链保持固定。MC/FEP在2002年实现了突破，当时Ulmschneider和Jorgensen在MCPRO程序中为MC模拟实现了具有柔性键长和二面角的协调旋转算法，这种实现允许在MC模拟中进行蛋白质主链采样并使得MC/FEP能够开始应用于蛋白质-配体体系。

AFE当前研究进展

在过去的20年中，随着计算机性能的增强和对计算研究的兴趣，人们已花费大量精力来改进CADD中的AFEM。我们无法总结所有贡献，但将重点介绍一些重要的研究进展，包括采样技术的改进以及力场的改进和自动化。除了所做的改进之外，我们还讨论了一些仍需解决的问题，以提高AFEM的效率。

为了在AFE计算中达到收敛性和准确性，对所有相关构象进行采样非常重要。但是，由于不同构象之间的势垒很大，因此在典型AFE计算的时间尺度上，采样通常是不完整的。因此，AFE计算结果通常取决于初始结构。目前已经有多种增强采样方法得到了开发，其中一种主要方法是将AFEM与副本交换方法（REM）耦合。温度REM涉及并行运行具有不同温度的MD或MC模拟的副本，最近开发了更有效的副本交换方法并将其与FEP结合使用，即采用溶质退火的副本交换（REST1和REST2）方法。对于标准FEP计算未能捕获构象变化的系统，已证明FEP/REST2可解决采样问题并能够精确再现实验性ΔΔAs。另一种增强采样的方法是使用图形处理单元（GPU）。最近，FEP、TI和MBAR都已经在GPU上得到了实现，并且伴随着2个数量级的加速，可以实现更多采样。随着计算机和GPU的性能不断增强，大型蛋白质-配体数据集上的AFE计算可以快速且常规地进行。

当前第二项重大进展是在力场方面。用于类药物有机分子的第一代力场是在1990年代末和2000年代初开发的，包括Merck大分子力场、OPLS、GAFF和CHARMM中的CGenFF。使用基于GPU的FEP/REST2方法和OPLS2.1力场的FEP+程序（Schrödinger, Inc.）针对八个蛋白-配体靶标进行了追溯验证。在八个系统上观察到的平均误差约为1 kcal/mol，并且据报道还为两个前瞻性药物设计项目可靠地预测了真正的阳性化合物。最近，GAFF v1.8力场与AMBER蛋白力场FF14SB相结合使用AMBER GPU TI实现针对相同的数据集进行了验证。与实验相比，所计算的ΔΔAs的RMSE（0.62–1.83 kcal/mol）与通过GPU FEP/REST2和OPLS2.1力场进行计算获得的RMSE（0.93–1.41 kcal/mol）相当。通过重新拟合肽的二面角参数以及配体电荷模型的改进，Harder及其合作者基于OPLS2.1力场开发了OPLS3力场。最近，对配体二面角类型的进一步广泛优化和对配体部分电荷分配的优化导致了OPLS3e力场得以报道。使用GPU FEP计算对前面八个蛋白质-配体数据集测试了OPLS3和OPLS3e力场，两者均显示出明显改善，RMSE分别为0.70–1.25 kcal/mol和0.63–1.17 kcal/mol。

GAFF2是基于GAFF开发的，其包括的范德华相互作用、键长、键角和二面角参数的重新参数化有望进一步改善力场。最近，分别使用Flair中的MBAR和GROMACS中的非平衡TI对GAFF2结合AMBER蛋白力场（FF14SB和FF99SB-ILDN）在大型蛋白质数据集上进行了测试，对于AMBER FF14SB/GAFF2和AMBER FF99SB-ILDN/GAFF2，前面提到的八个蛋白质-配体测试集的RMSE分别为0.29-1.68 kcal/mol和0.90-1.56 kcal/mol。所有测试均表明，当前的类药物分子力场与不同的AFEM结合使用的性能对于回顾性研究结果是令人满意的。

当前力场使用原子类型来描述不同化学环境中的不同原子，然后根据原子类型分配不同的非键合和键合参数。CADD中AFEM的一个主要问题是，在药物开发项目中，类药物配体的化学空间很大，以至于现有的力场可能无法覆盖所有的配体原子类型。因此，需要进一步的原子类型和参数化工作来解决这一缺陷。最近，一种新的力场格式，即SMIRKS Native Open Force Field（SMIRNOFF）格式，被用于开发开放力场模型。使用SMIRNOFF格式时，力场参数是通过直接化学感知分配的，而不是基于原子类型的。新格式具有更大的灵活性和简便性，并且还可以避免基于原子类型的力场出现某些问题。另一种力场，即QUantum mechanical BEspoke（QUBE）力场也可以规避传统力场的参数传递性问题。QUBE力场从QM电子密度得出系统特定的非键合参数。目前它已被用于研究蛋白质-配体结合自由能以及蛋白质动力学，并显示出令人鼓舞的结果。

最后也是十分重要的一项进展是自动化。此前设置不同类型的自由能计算可能十分不方便、耗时且容易出错，因此使这些方法更易于使用的关键步骤是简化设置，运行模拟然后分析结果。目前已经开发了许多工具可以帮助自动执行AFE计算的各个阶段，使用这些工具和程序，可以以更快、更可靠的方式执行大规模计算的设置和分析，这将大大有利于AFEM在制药领域中的应用。但是，尽管可以使用多方位检查来评估AFE计算的可靠性，包括向前和向后扰动的滞后、周期闭合错误以及相邻的λ窗口之间的重叠，亲自实践的经验仍然扮演着十分重要角色。因此还需要用户在相关领域的专业知识和培训，例如对程序适用范围的理解，如果一切自动化，用户将失去对设置模拟详细信息的控制权，这可能会导致意外或意外的结果。

总结

总而言之，在过去30多年的时间里，我们在发展AFEMs方面的经验有起有落，但可以相信通过最终的努力，我们最终可能会拥有一种能够可靠地加速药物开发的工具。最后的努力包括解决在工业环境中进行AFEM的一些剩余的关键的挑战。Merck KGaA在最近关于AFEM的实际使用的研究中，列出了在药物设计过程中使用AFEM时遇到的一系列问题。这些问题包括由于构象变化引起的蛋白质结构不确定性，配体结合模式的不确定性，X射线结构中缺失的成分，测定条件和模拟条件之间的差异，金属和辅因子以及蛋白质和配体的质子化状态的不确定等。此外，对配体互变异构的正确处理仍然是一个挑战，还有对于AFE计算，涉及电荷变化、骨架变化、芳环到脂肪链等的扰动也带来了一系列挑战。随着计算能力的不断提高和新型分子表示形式的出现，未来几年AFE计算技术的发展必将更加完善。

参考文献

Lin Frank Song and Kenneth M. Merz, Jr.* Evolution of Alchemical Free Energy Methods in Drug Discovery. Journal of Chemical Information and Modeling. 2020. DOI: 10.1021/acs.jcim.0c00547