
引言
当今炼金术自由能计算方法已经被广泛应用于小分子先导化合物的优化过程中,计算精度已经达到了1 kcal/mol左右。尽管如此,在已发表的研究中使用自由能计算来推动作用于两个相似靶标的化合物的选择性优化方面相对较少。在最理想的情况下,配体结合位点的相似性可能会导致误差的偶然消除进而可以比亲和力更准确地预测其选择性。在这里,结合人类激酶CDK2和CDK9之间非常相似的结合位点以及从另一个系列的配体中找到针对关系相对较远的激酶CDK2和ERK2的选择性配体的基础上,本文系统性地评估了针对小分子激酶抑制剂选择性预测的准确性。通过使用贝叶斯分析方法,作者将系统误差与统计误差分开,并对选择性靶标之间系统误差的相关性进行量化,进而发现在CDK2/CDK9的例子中,系统误差的高度相关性表明自由能计算可以对化学家实现选择性带来较大帮助,而在更远相关的激酶(CDK2/ERK2)中,系统性误差的相关性表明在不那么密切相关的系统之间甚至可能发生偶然的消除(fortuitous cancellation)。在这两种情况下,系统误差的相关性都表明更长时间尺度的模拟有利于适当地平衡统计误差与系统误差,以充分利用选择性预测中自由能计算精度提高的优势。
选择性是药物设计中的重要考虑因素
除了效能(potency)外,选择性也是药物开发中重要的特性。控制选择性不仅可以避免脱靶毒性(抑制非预期靶标),而且还可用于避免靶上毒性(抑制预期靶标)。在任一种情况下,考虑化合物的选择性都会因靶标的生物学而变得复杂。例如,激酶作为复杂信号网络中的节点存在,具有反馈抑制和路径间的串扰。仔细考虑哪些脱靶被抑制可以避免由于减轻反馈抑制作用而引起的脱靶毒性,以及通过缓解串扰抑制而无意中重新激活了靶途径或次级途径的上调。脱靶毒性也可能是由于抑制不相关的靶标,例如吉非替尼(一种EGFR抑制剂),也抑制CTP2D6,从而对肺癌患者造成肝毒性。在癌症环境中,可以通过考虑激酶的致癌突变体形式相对于野生型形式的选择性来避免靶向毒性,例如许多第一代EGFR抑制剂。
激酶是选择性预测重要
且极具挑战性的模型系统
激酶是一种有用的可以用来评估自由能计算在药物发现背景下预测抑制剂选择性的效能的模型。随着伊马替尼在2001年批准用于治疗慢性粒细胞性白血病,靶向小分子激酶抑制剂(SMKIs)已成为治疗癌症和其他疾病的主要疗法。目前,已有62种FDA批准的SMKIs,且针对激酶的疗法占当前药物开发的50%。尽管已经获得了许多成功的药物批准,但目前FDA批准的激酶抑制剂仅靶向与疾病有关的一小部分激酶,而针对新型靶点设计新的选择性激酶抑制剂仍然是一项重大挑战。这主要是由于有超过518种蛋白激酶共享大多数SMKIs靶向的高度保守的ATP结合位点。虽然激酶抑制剂已设计为靶向激酶特异性亚口袋和结合模式以实现选择性,但先前的研究表明,I型(与活性DFG-in构象结合)和II型(与无活性DFG-out构象结合)抑制剂能够实现一定范围的选择性,除了其主要靶标外,通常还表现出与许多其他靶标的显著结合。
炼金术自由能方法
可用于预测化合物的选择性
尽管配体i对单个靶标的效价通常可以被量化为结合的自由能(ΔGi),但仍有许多不同的指标可用于量化化合物的选择性。在这里,我们将一个目标与另一个目标(一个反目标)之间的选择性Si视为两者之间给定配体i的结合自由能之差。
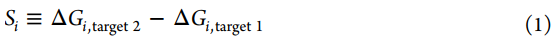
在优化效能时,我们关注的是ΔΔGij≡ΔGj–ΔGi,即配体i和j与单个目标结合的相对自由能,而在选择性的优化中,我们关注的是ΔSij≡Sj–Si,反映了配体i和相关配体j之间的选择性变化。
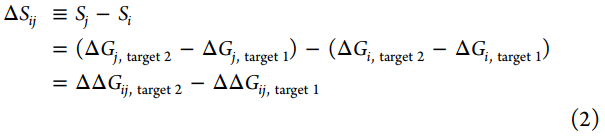
为了预测两种相关化合物之间选择性ΔSij的变化,我们开发了一种使用相对结合自由能计算(FEP+)来构建同类型中配体之间的炼金术扰动图的方法。对于每个感兴趣的目标,每个配体(节点)之间具有相同的扰动(边缘),每个边缘代表一个相对的炼金术自由能计算,该计算量化了单个目标的配体(节点)之间的ΔΔG。通过这些计算,我们可以计算出两个感兴趣的目标之间的选择性变化ΔSij,这是通过将配体i转换为配体j来实现的。由于每个目标的模拟计算是分开的,如果我们假设两个目标的系统误差均按照双变量正态分布进行分布,其中相关系数ρ量化了相关程度(其中ρ=0表示不相关,ρ=1表示完全相关,ρ=-1表示完全反相关)和两个目标(σstat,ij,target)的统计误差是完全独立的,我们可以将预测ΔSij的误差建模为σ选择性。
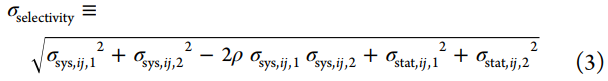
系统误差的相关性
可以显著提高选择性预测的准确性
为了证明相关系数ρ对使用炼金术自由能技术预测选择性的潜在影响,我们根据等式3建立了一个简单的数值模型,其中考虑了每个目标系统误差(σsys,ij,1和σsys ,ij,2),如图1A所示,如果每目标系统误差的大小相同(σsys,ij,1 =σsys,ij,2),则即使单目标效能系统误差为非零,σ选择性也将接近0,而相关系数ρ接近1。如果自由能方法的误差在大小上不相同(σsys,ij,1≠σsys,ij,2),则σ选择性变小,但随着ρ接近1而接近非零值。同时为了量化达到所需的选择性阈值而必须合成的化合物数量的预期减少量(以下称为选择性优化中的加速作用),我们对多种化合物的选择性相对于参考化合物的变化进行了建模。药物化学家可能会建议以0为中心的正态分布,标准偏差为1 kcal/mol(图1B,黑色曲线),这反映了这样一种观念,即大多数提议的修饰都不会驱动选择性的大变化。合成化学家的方案分配可以建模为正态分布的这一假设是基于Abbott实验室对效能变化分析的数据驱动估算得出的。合成所有预测具有1.4 kcal/mol或更高的选择性(亲和力比为10倍)的化合物,并使用具有完美测量精度的实验技术进行实验测试(图1B,彩色曲线)。可以计算出与原始分布相比具有真正的1.4 kcal/mol选择性提高的化合物比例的倍数变化,可以作为预期加速比的替代物。对于这个1.4 kcal/mol的选择性提高阈值,相关系数ρ= 0.5给出了4.1倍的预期加速比,这可以解释为需要减少4.1倍的化合物以使选择性提高10倍。此过程可以扩展为实现选择性提高100倍的效果(图1C),其中可以预期200-300倍的提速,具体取决于单目标系统误差(σsys,ij,target)。如图1D所示,更严格的合成规则与高相关系数(ρ)相结合,只要已经对足够的化合物进行了打分,自由能计算对设计选择性抑制剂的影响最大。有趣的是,在相关系数ρ=0.75且打分化合物较少的情况下,与1000x合成规则相比,500x合成提供了更高的加速比。这是因为在对更多化合物进行打分之前,没有任何化合物符合更严格的1000x合成规则。这对药物发现工作显然是有影响的,因为时间和计算资源可能会限制能够用自由能方法分析的化合物的数量。
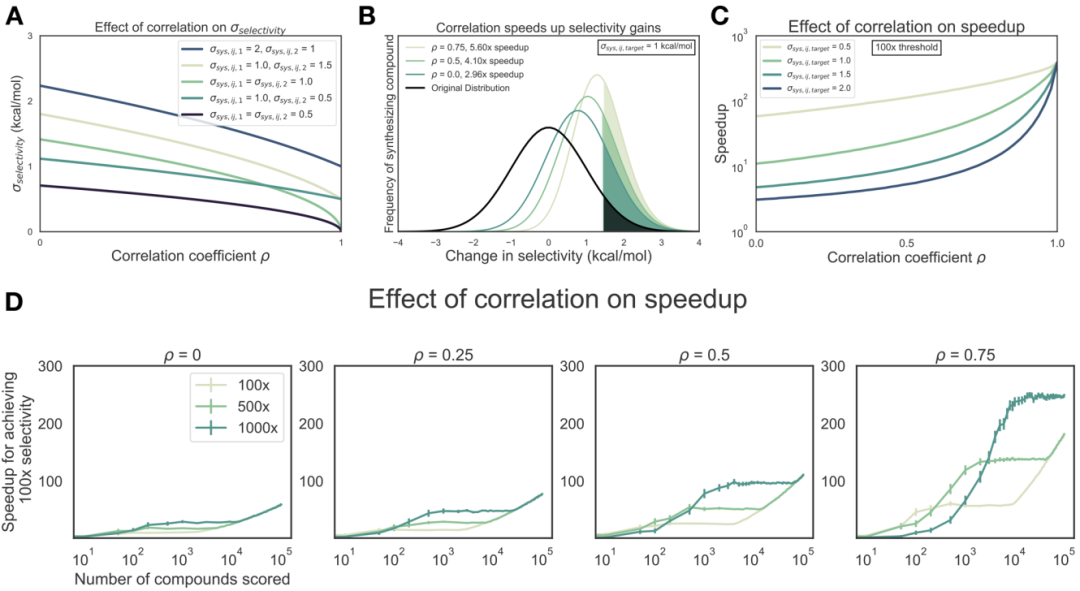
图1 自由能计算可以加速选择性优化
图片源自JCIM.
CDK2/CDK9抑制剂的实验数据集
证明了实现高选择性的难度
为了评估自由能预测中误差与选择性的相关性,我们着手收集符合许多标准的数据集。我们收集的数据集除了包含具有相同配体的每个靶标的晶体结构外,还包含许多激酶靶标和配体的结合亲和力数据。基于激酶-配体相互作用指纹和结构(KLIFS)数据库中鉴定的85个结合位点残基的多序列比对,CDK2和CDK9具有57%的序列一致性。对于此CDK2/CDK9数据集,根据在同行论文中发表的工作,将配体12c与CDK2/cylin A(图2A,左)和CDK9/cyclin T(图2B,左)共结晶。在CDK2和CDK9中,配体12c与激酶形成相对少的氢键相互作用。对配体12c的亲和力稍低的CDK9(图2C,右)在配体12c的磺酰胺基团和残基E107之间形成相互作用。另一方面,CDK2在配体12c的磺酰胺基团与残基K89和H84之间形成相互作用。同类的配体系列包含许多困难的扰动,尤其是在取代基R3处(图2C,左)。
这一同类的配体系列还突出了使用公开数据进行工作的两个挑战:首先,选择性的动态范围非常窄,平均值S(CDK9–CDK2)为-0.65 kcal/mol,标准偏差仅为0.88 kcal/mol,使得该数据集的总动态范围为2.8 kcal/mol。其次,没有报告实验测量的实验不确定性。该数据集报告了使用Km(ATP)测得的CDK2和CDK9的IC50计算得出的Ki值,以及使用Cheng-Prussof方程进行测定得出的[ATP]。因此,因此,对于这组配体和后续配体,根据先前所做的总结实验数据不确定性的工作,假设没有系统实验误差,则随机实验不确定性假定为0.3 kcal/mol。
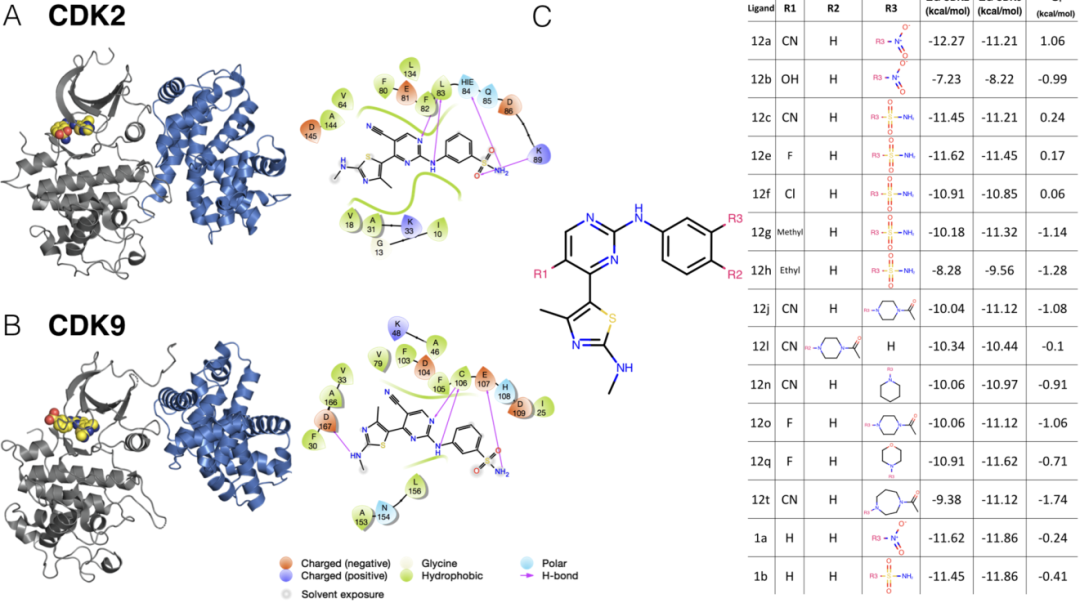
图2 CDK2/CDK9数据集展现密切相关的激酶之间的选择性优化
图片源自JCIM.
CDK2/ERK2抑制剂的实验数据集
如何实现了更高的选择性
基于KLIFs结合位点残基的多序列比对,CDK2和ERK2具有52%的序列一致性,使其与CDK2和CDK9(57%)的关联度略低。虽然所有这三种激酶都属于CMGC家族,并且在系统发育树中密切相关,但CDK2和CDK9属于CDK(细胞周期蛋白依赖性激酶)亚家族,而ERK2是邻近的MAPK(促分裂原激活的蛋白激酶)亚家族的一员。从结构的角度来看,本研究中使用的两个激酶PDB对也非常相似。结合位点的叠加显示, CDK2/CDK9对的RMSD仅为0.81Å,而CDK2/ERK2对的RMSD仅为0.92Å。CDK2(图3A,顶部)和ERK2(图3B,顶部)的晶体结构都可与配体22共同结晶而获得。其中CDK2采用DFG-in构型,其中的α-C螺旋向外旋转,远离ATP结合位点,并破坏了K33和E51之间的保守盐桥,表明该激酶是无活性的。相比之下,来自CDK2/CDK9数据集的CDK2结构采用DFG-in构型,其中旋转了α-C螺旋,由于细胞周期蛋白A的变构激活,在K33和E51之间形成了指示活性激酶的离子锁。
这两种激酶之间的结合模式相似。在配体的骨架和一个铰链残基的主链之间(CDK2为L83,ERK2为M108)存在一组保守的氢键。保守的赖氨酸(CDK2为K33,ERK2为K54)通常参与与α-C螺旋形成离子锁的过程,在CDK2和ERK2中均与配体骨架形成氢键(图3A,B,底部)。但是,在ERK2结构中,羟基与CDK2结构中不存在的氢键网络中的结晶水以及N154有相互作用。同类配体系列具有单个溶剂暴露的取代基。这有助于解释选择性的狭窄分布,其平均选择性为-1.74 kcal/mol(ERK2-CDK2),标准偏差为0.56 kcal/mol;该数据集的总动态范围为2.2 kcal/mol。尽管较小的标准偏差表明用R-基团取代难以驱动选择性,但总动态范围表明R-基团取代可以显著提高选择性。
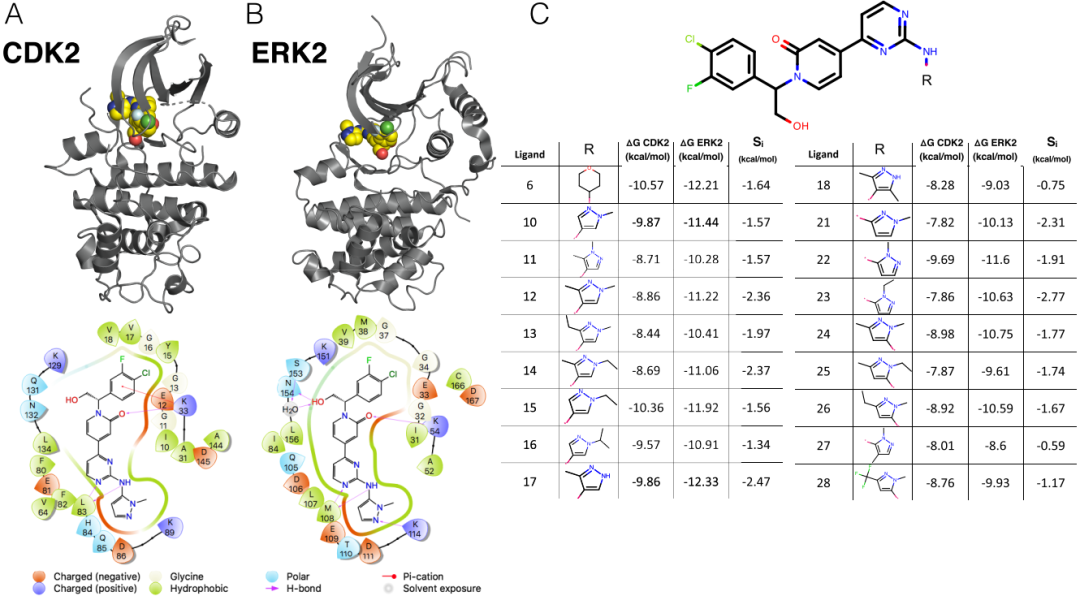
图3 CDK2/ERK2数据集展现相对不相关的激酶之间的选择性优化
图片源自JCIM.
系统误差的相关性加速了选择性优化
为了量化靶标之间系统误差的相关系数(ρ),我们建立了贝叶斯图形模型以将系统误差与统计误差分开,并量化我们对ρ估计值的置信度。CDK2/CDK9计算显示出强有力的相关性,相关系数为0.69(图4A,右)。尽管每个靶标系统误差较高,但CDK2/CDK9计算的错误高度相关性导致1 log10单位选择性优化的速度提高了3倍,2 log10单位选择性优化的速度提高了10倍。CDK2/ERK2计算的相关系数ρ量化为0.48,表明误差在ERK2和CDK2之间有中等相关性(图4B,右)。考虑到加速模型中其中打分和合成的化合物数量不受限制,对于CDK2/ERK2计算,适度的相关性和较低的每个靶标系统误差允许1 log10单位选择性优化的预测的4-5倍加速和2 log10单位选择性优化的30-40倍加速。
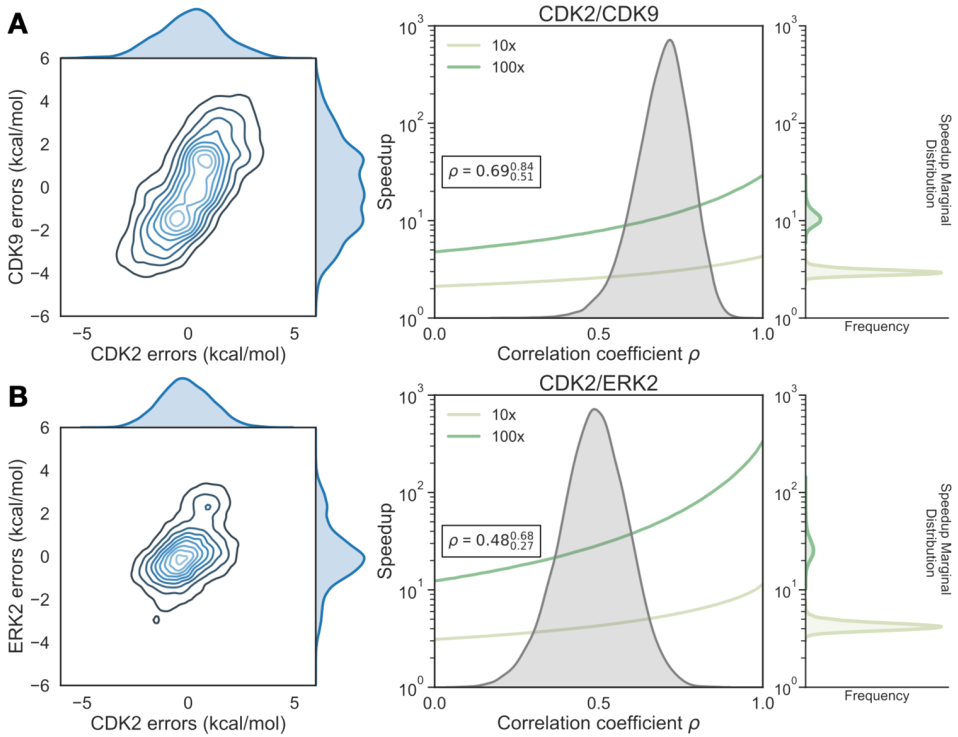
图4 靶标之间系统误差的相关性可以显著加速选择性优化
图片源自JCIM.
总结
1) S是先导化合物优化中选择性的有用指标。有许多不同的指标用于量化化合物的选择性,最早的指标之一是标准选择性分数,还有采用热力学方法来研究激酶的选择性。在这里,我们提出了一种更精细的从热力学角度来说明选择性的方法,即可以使用自由能计算方法直接计算:两个不同靶标之间给定配体的结合自由能的变化(S),其目标是使用物理模型来改善或维持先导化合物系列中的选择性。
2)系统误差相关可以加速选择性优化。尽管预期的加速取决于该方法的每个靶标的系统误差,但加速也高度取决于两个目标的误差相关性。在更实际的情况下,打分和合成的化合物数量受到资源的限制,我们已经证明了使用相同的数值模型,更严格的合成规则会导致自由能计算的加快。
3)两对激酶测试系统表明系统错误可以关联。尽管CDK2和ERK2属于不同的激酶亚家族,但系统误差中的计算相关性表明,与同一亚族中密切相关的激酶相比,偶然消除误差可能适用于更广泛的场景。这可能是由CDK2和ERK2之间相对较高的结合位点序列一致性驱动的(52%,而CDK2/CDK9为57%)。但是,相关性的置信区间很宽,这表明与更远距离相关的蛋白质的误差将只有中等相关性。
4)当系统错误相关时,减少统计错误是有益的。除非相关系数ρ对两个感兴趣的靶标高度正相关,否则运行更长时间的计算不会有太多好处。但是,当通过相关性减少系统误差时,较长时间的计算可以帮助实现加速的大幅增加,以实现提高选择性的目标。在进行化合物制备和测试预测时,对自由能计算保持ρ的连续定量化,可以决定进行更长时间的计算是否值得。
5)更大的蛋白质靶标数据集将对未来的工作十分有用。本文收集的数据集受到化合物总数、选择性(S)的小动态范围以及缺乏可靠的实验不确定性的限制。小的数据集使得很难得出关于系统误差相关性的广泛结论。要了解基于结构或序列相似性的先验相关程度,需要研究的靶标范围比本研究中介绍的两对靶标更大,包含许多蛋白质靶标、晶体结构和定量结合亲和力数据的较大数据集将是十分理想的。本工作表明系统误差中的相关性可以允许自由能计算,以促进药物发现项目选择性优化中的显著加速。
参考文献
Steven K. Albanese, John D. Chodera, Andrea Volkamer, Simon Keng, Robert Abel, and Lingle Wang. Is Structure-Based Drug Design Ready for Selectivity Optimization? J. Chem. Inf. Model. 2020. DOI: 10.1021/acs.jcim.0c00815