蛋白质结合口袋(protein binding pockets,以下简称口袋)是指蛋白质表面或内部具有适合与配体结合的空腔,口袋周围的氨基酸残基决定了它的形状,位置,物化特性以及功能[1]。口袋的动力学对蛋白质的特异性相互作用至关重要。蛋白质结构的柔性(flexibility)与运动(mobility)允许结合口袋的打开、关闭和适应,从而调节配体的结合过程和发挥特定的蛋白质功能。这意味着在预测结合性能以及设计新配体时必须考虑蛋白质的内部运动。
(一) 口袋动力学的分类
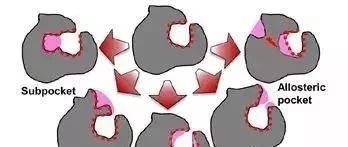
蛋白质结构的柔性对口袋的影响可分为五种不同类型(图1)
(1)子口袋(subpocket)的出现/消失
(2)邻近口袋(adjacent pocket)的出现/消失
(3)呼吸运动(breathing motion),指初始口袋的扩大或收缩,大致保留初始口袋的形状
(4)通道/隧道(channel/tunnel的打开/关闭,可将蛋白质内的口袋与溶剂连接,包括盖子(lid)的运动
(5)变构口袋(allosteric pocket)在某个位置出现或消失
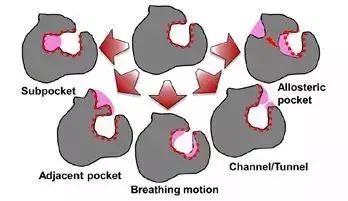
图1:五种不同的口袋动力学示意图
以下使用具体例子说明这五种类型。
(1)子口袋
热休克蛋白(HSP90)N端的ATP结合区,没有配体时,口袋橙色部分中间为loop,结合配体后(蓝色)形成α-helix,下面疏水部位即子口袋。PDB ID: 1yer,1uyd。(图2)
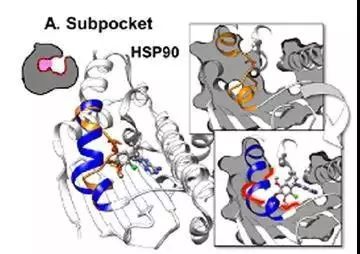
图2. 子口袋的形成
橙色和蓝色为导致变化的部位,灰色为蛋白质内部,红色为口袋的变化,下同。
(2) 邻近口袋
白介素(IL-2)具有高度适应性的蛋白结合位点,可被小分子阻断,在蛋白结合位点附近的表面有一个柔性疏水子口袋,当结合小分子抑制剂时,侧链旋转,骨架微调(红色),形成邻近口袋,为结合小分子抑制剂提供了额外的空间。PDB ID: 1pw6,1m4a。(图3)
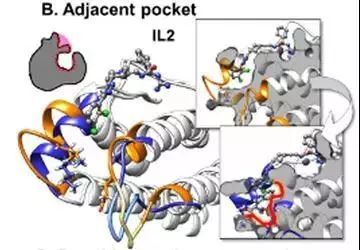
图3. 邻近口袋的形成
(3) 呼吸运动
抗凋亡蛋白(BCL-XL)口袋周围的α-helices在结合不同配体是会发生较大的变动,当较小的配体结合时,口袋较小(橙色),当较大的配体结合时,口袋有较大的舒张(蓝色)。PDB ID: 3zln,3qkd。
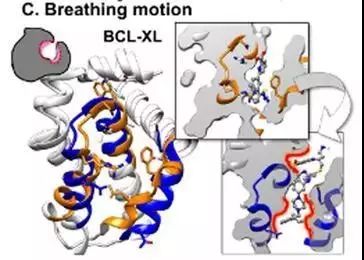
图4. 呼吸运动
(4) 通道/隧道
核磁共振(NMR)结构显示非特异性脂质转运蛋白(ns-LTP )结合配体前列腺素B2 (prostaglandin B2)时的通道的打开(蓝色)与关闭(橙色),PDB ID: 1cz2模型2与8。
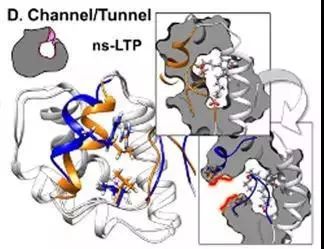
图5. 通道的打开
(5) 变构口袋
P38有丝分裂原活化蛋白激酶(P38 MAPK)中保守的Asp-Phe-Gly motif运动形成变构口袋。Phe侧链向ATP/ADP结合位点翻转,打开变构口袋,减少了结合位点的体积,因此,在变构位点的抑制剂结合可抑制ADP/ATP结合。PDB ID: 1kv1,1ny3。
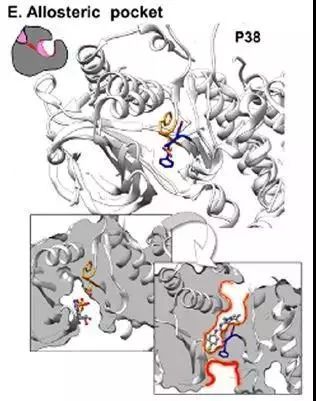
图6. 变构口袋的形成
以上五种分类在具体的口袋变化中是可能重叠的。比如说,形成子口袋前可能先发生呼吸运动;当变构口袋邻近初始口袋时也可认为是邻近口袋。邻近口袋的位置特点使得二价配体能同时结合两个口袋。
(二)口袋的识别
通过实验方法得到带配体的蛋白质结构,其配体的位置可用来定义结合口袋。另外也可用计算机方法进行识别。
实验方法
这里主要介绍几种常见的蛋白质结构解析方法。
(1) X射线晶体学(X-ray crystallography)
X射线击中晶体产生散射束,由探测设备记录其衍射数据,进而计算电子密度图,这些电子密度图能够用来计算蛋白质结构信息,最终得到蛋白质构象。该方法可得到高分辨率的蛋白质静态三维结构,另外还可得到原子振动信息,如B-factor。但在解决大分子蛋白质上具有局限性,并且通常依赖于同源蛋白质的结构信息。截至目前PDB中89.30%蛋白质结构用该方法测定。
(2) 核磁共振波谱学(nuclear magnetic resonance,NMR)
不同原子具有不同的核磁共振吸收波谱能力,根据原子波谱性质将通过核磁共振实验收集的原始数据计算转化成蛋白质结构和动力学信息。该方法在溶液中和非晶态的蛋白质进行测量,能够获得高分辨率蛋白质静态三维结构信息,而且能够获得某些构象转换的动力学信息。但是大尺寸蛋白质的磁化信号难以测量。截至目前PDB中有8.22%%蛋白质结构用该方法测定。
(3) 三维电子显微镜(3D Electron Microscopy,3DEM)
近年来兴起的,同时也是最常用的3DEM技术为冷冻电子显微技术(cryo-EM),优点在于能够获得蛋白质自然条件下的结构信息,更接近于蛋白质在生物系统中的真实结构并且能够获得超大规模蛋白质或蛋白质复合体的结构信息,如病毒等。截至目前PDB中2.14%蛋白质结构使用3DEM方法测定。
计算方法
计算机方法识别蛋白质口袋主要基于几何特征与生化物理特征的结构分析。几何特征一般包括三维网格(grid)、空间球体(sphere)、α-share理论,和数学形态学理论。生化物理特征一般包括结合能和蛋白质的序列保守性等物理化学属性和生物学属性。
(1) 基于网格的预测算法(e.g. POCKET,LIGSITE,LIGSITEcs,Q-SiteFinder)
POCKET是最早的基于网格的一种预测算法,前后改进发展出LIGSITE与LIGSITEcs。这种算法的理论依据是小分子倾向于结合在蛋白质表面大而深的口袋型区域。POCKET、LIGSITE和LIGSITEcs分别扫描网格中的蛋白-溶剂型-蛋白和表面-溶剂型-表面事件,满足条件的节点则表示具有一定的埋藏度(buriedness)。POCKET使用3个方向,后两者使用7个方向,POCKET、LIGSITE使用的是原子坐标,而LIGSITEcs使用的是康诺利表面(connolly surface)。(康诺利表面是表示蛋白质分子光滑的曲面的模型,由蛋白质分子表面部分与探针分子相切原子的范德华表面连接在一起形成的)。Q-SiteFinder类似于LIGSITE,但pocket位点的排序是探针与蛋白原子之间的范德华相互作用能之和。
(2) 基于球体的预测算法(e.g. SURFNET, PASS)
SURFNET是在两个原子之间放置了一个球体,球体与这两个原子的范德华表面相切。如果这个球体与其他原子的范德华表面有交集,那么缩小球体的半径,使它不能包含任何原子。体积最大的球体定义了最大的口袋。
PASS与SURFNET的算法不同,是一种只在蛋白质表面初始化球体的方法。它先将探针球包裹在蛋白质表面,去除无法满足埋藏数(burial number)的球体,埋藏数是球体周围8Å之内的蛋白质原子的数目。然后重复操作,直到没有新的探针球被保留,活性位点(ASPs)根据埋藏数的大小以及周围的球体个数确定。
(3) 基于α-share理论的预测算法(e.g. CAST)
CAST采用三维理论将蛋白质的三维结构描述成为由许多的三角形的构成的网。蛋白质中的原子构成了三角形的顶点。然后通过将小的三角形合并到邻近的大的三角形进行聚类,结合位点就是最后得到的空的三角形的集合,即内部不包含其他原子。
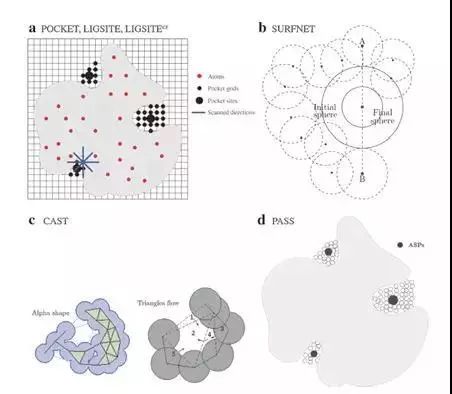
图7. 不同口袋识别方法示意图[2]
宏算法Metapocket 1.0综合了LIGSITEcs, PASS,Q-SiteFinder, 和 SURFNET四种传统预测算法进行口袋预测[3],2.0版本又添加了另外四种传统预测算法Fpocket、GHECOM、ConCavity、POCASA,其在预测成功率上最多可以比传统算法提高12%,Metapocket2.0与其他预测口袋算法可参见文献[4]。
(三) 蛋白质口袋构象采样
实验可能无法获得所有可能影响化合物选择性的构象。计算方法可以填补这些空白。对上述五类口袋动力学,MD模拟都适用,其精准度高但计算量大,并且在模拟时长内可能无法对口袋动力学进行充分的采样,因此,其他一些计算效率更高但精度较低的方法也被用于研究大规模蛋白质运动引起的蛋白质结合口袋动力学。以下对两种基于约束几何模拟的方法进行介绍。
tCONCOORD[5]
tCONCOORD是对CONCOORD[6] (fromCONstraints to COORDinates)的扩展,CONCOORD先对实验获得的蛋白质结构所有成对的原子间距离进行测量。距离约束限制设定在±Dnm。相互作用紧密的,D值较小,相互作用弱的,D值较大。不同类型的相互作用对应不同的距离限制D,之后通过随机产生满足约束条件的结构。tCONCOORD将估算氢键稳定性纳入约束定义中。实验上结构显示,蛋白质发生构象转变时通常涉及一个或多个氢键的打开。保持氢键“干燥(dry)”环境是构象稳定性的先决条件,蛋白质的折叠与周围疏水基团对氢键的系统“脱溶(desolvation)”效果有关。因此,分析一个特定氢键的邻域可以为水分子攻击它的概率提供线索,而水分子攻击它的概率与构象打开概率直接相关。tCONCOORD通过估计溶剂化概率来预测不稳定氢键。通过计算MD模拟后的多种蛋白质的每种原子的径向分布函数(RDF,Ri),加权后生成的值Pi,作为溶剂化参数来估计特定原子的特定距离内找到水分子的概率。
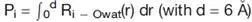
得到的溶剂化参数用于评价特定氢键的周围环境。周围环境是以氢和受体原子为中心,半径6 Å(排除三个键长外的原子)的区域,然后计算溶剂化分数。

溶剂化分数越大表示该区域越不稳定,超过一定阈值的区域则在后续结构生成时不加约束条件,阈值的设置参考见图8,具体的阈值根据研究体系与研究目的而改变。结构的生成是从随机坐标开始构造结构,迭代地对原子的位置进行修正,直到满足所有的约束条件。因为每次运行都是从随机坐标开始的,所以每个新生成的结构都完全独立于前一个结构。故无法得到从一个构象到另一个构象的路径的信息,也没有关于两个构象态之间的势能信息。
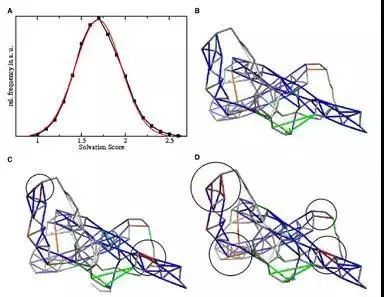
图8. tCONCOORD阈值的设置
A. 290个蛋白质结构氢键溶剂化分数的分布;B. 以人类朊蛋白为例(PDB: 1QM0),氢键的分布情况,骨架之间的氢键(蓝色),骨架与侧链之间的氢键(橙色),侧链之间的氢键(绿色);C. 阈值设置为2.2时检测到的不稳定的氢键(黑圈中红色部分);D. 阈值设置为2.1检测到的不稳定的氢键,数量比C中更多。
FRODA[7]:The framework rigidity optimized dynamic algorithm
若将蛋白视为网络结构,那么共价键键长,键角,共价双键,氢键与疏水作用都是受约束的, 蛋白质形状的改变则发生在可旋转的二面角。FRODA首先使用FIRST中的pebble game algorithm对蛋白进行刚性分析判定决定刚性部位与可旋转的二面角。若将蛋白比做‘body-bar’,每个原子最开始都有六个自由度,每中限制类型带来一定数量的“bar”,也就减少对应的自由度“pebble”,其中疏水作用2“bar”,单共价键或氢键5“bar”,Locked的共价键(double, peptide/aromatic)6“bar”。 “bar” 多的区域为“stressed”, “bar” 等于“pebble”的区域为isostatic,“pebble”多的区域为flexible。接着用虚构的刚性体(ghost templates)替代原子间相互作用(图9),ghost模板的位置和方向通过最小二乘法确定。然后通过对所有原子进行随机位移,在约束下过通过迭代过程探索构象变化的相空间。迭代可分为3步骤,将ghost模板匹配到原子位置,原子匹配到ghost模板,分子在空间上回到正确的新构象(图10)。
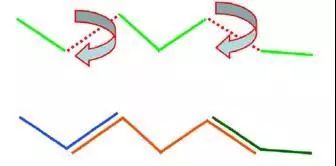
图9. ghost模板示例
一个具有两个可旋转二面角的聚合物链(上)与三个重叠的ghost模板(下)相关联。每一组互相为刚性的原子属于共同的ghost模板,而与一个可旋转键相关联的原子则属于多个ghost模板。
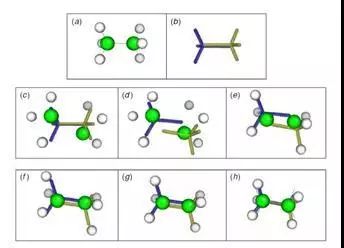
图10. ghost模板约束条件下的迭代过程
由几何模拟确定的乙烷分子的运动。
(a)初始原子位置
(b) ghost模板
(c)随机原子位移
(d)将ghost模板拟合到原子上
(e)将原子拟合到ghost模板
(f)和(g)重复(d)和(e)的迭代
(h)直到找到新的构象
研究口袋动力学的方法还有很多,不同方法具有不同的适应范围。例如MDPocket,PocketAnalyzer,EPOSBP,TRAPP等适用于探索邻近口袋、子口袋和呼吸运动的形成,SPACER和MCPath适用于变构口袋的检测与分析,Caver 3.0可用于描述MD轨道中的隧道(tunnel)。另外,不同的口袋动力学对配体结合过程具有在热力学和动力学上具有不同的影响。
参考文献
1. Stank A, Kokh DB, Fuller JC,Wade RC. Protein Binding Pocket Dynamics. Acc Chem Res. 2016;49(5):809-15.
2. Huang B, Schroeder M.LIGSITEcsc: predicting ligand binding sites using the Connolly surface anddegree of conservation. BMC Struct Biol. 2006;6:19.
3. Huang BD. MetaPocket: A MetaApproach to Improve Protein Ligand Binding Site Prediction. Omics-a Journal ofIntegrative Biology. 2009;13(4):325-30.
4. 张增明. 蛋白质—小分子结合位点预测新算法研究开发 [硕士]: 浙江大学; 2012.
5. Seeliger D, Haas J, de GrootBL. Geometry-based sampling of conformational transitions in proteins.Structure. 2007;15(11):1482-92.
6. de Groot BL, van Aalten DM,Scheek RM, Amadei A, Vriend G, Berendsen HJ. Prediction of proteinconformational freedom from distance constraints. Proteins. 1997;29(2):240-51.
7. Wells S, Menor S, Hespenheide B, Thorpe MF. Constrained geometricsimulation of diffusive motion in proteins. Phys Biol. 2005;2(4):S127-36.
转载自QMCLab:蛋白结合口袋动力学的分类与识别方法