Nat Chem | 用深度学习方法求解薛定谔方程

结果

DNN电子波函数拟设

作者对电子薛定谔方程的深度学习解法的核心是一个称为PauliNet的波函数拟设，它既包含了可以很好地描述电子波函数的基本物理学方法——Slater行列式、多行列式扩展、Jastrow factor、backflow transformation和尖峰（cusp）条件，也包含了能够编码异质分子体系中电子运动的复杂特征的DNN。作者提出的波函数属于多行列式Slater-Jastrow-backflow类型。 

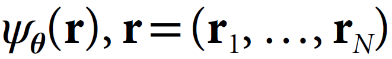
其中，Jastrow factor J，和backflow f都由DNN表示，可训练参数为θ （图2）。这些DNN为PauliNet提供了卓越的表示能力，而行列式、单电子分子轨道φ_μ、及电子尖峰γ组成了PauliNet的物理基础。

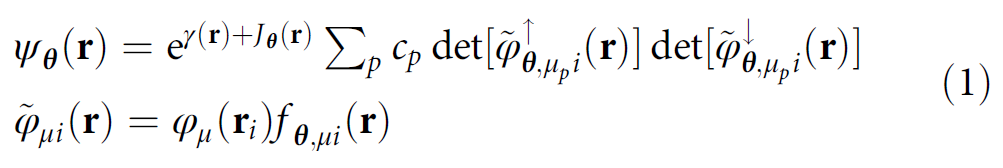
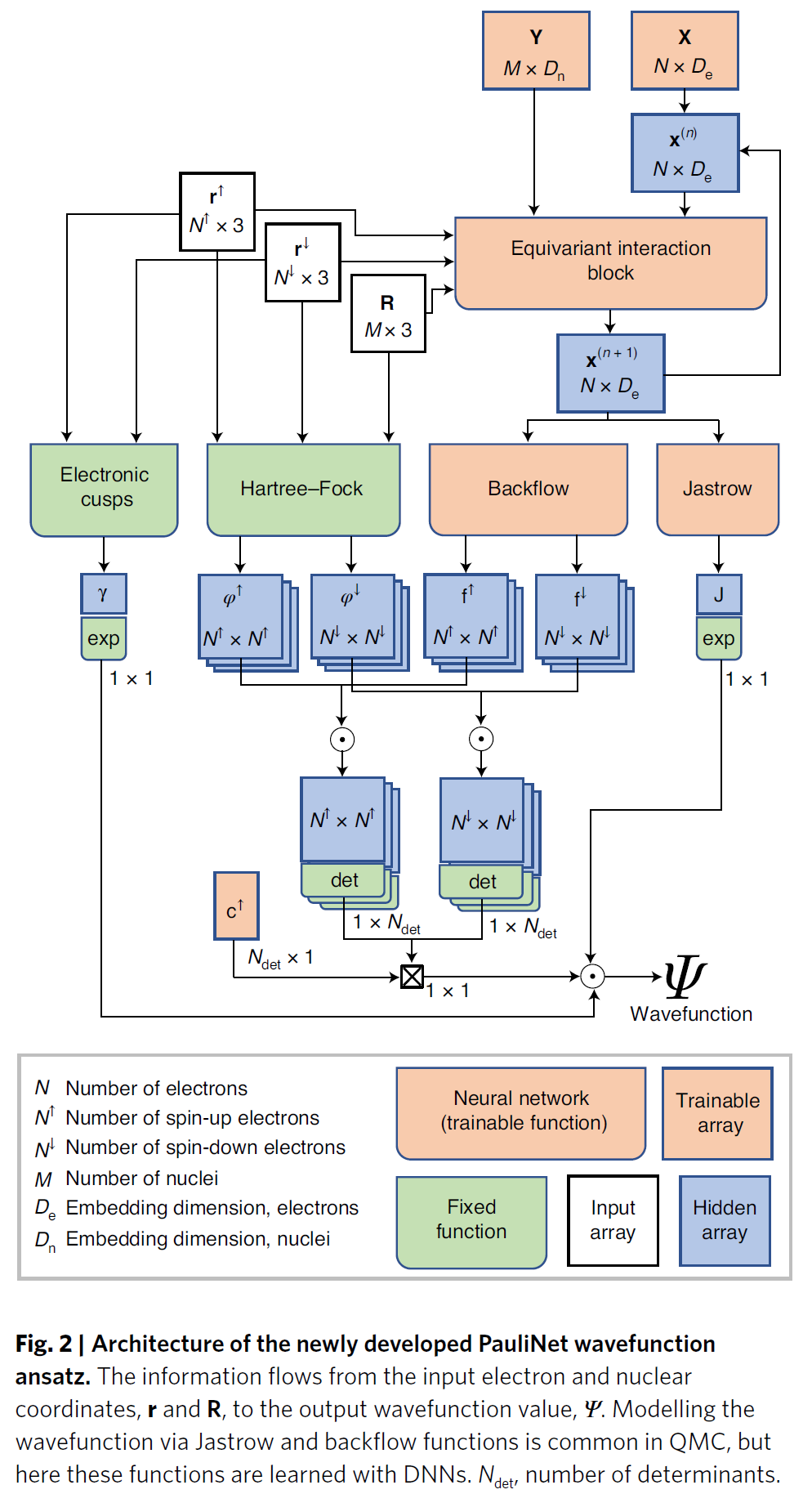
图2 PauliNet架构

数据来源：Nature Chemistry

每个有效的电子波函数都必须相对于自旋电子的交换是不对称的，一如量子化学中常见的方式，作者通过矩阵行列式实现反对称性，因为行列式在交换任何两行或两列时都会改变符号。

为确保变分优化问题的良好起点，作者采用了近似HF方法。具体来说，作者使用具有较小完整活动空间的多参考HF计算，并根据其线性系数的大小选择最主要的行列式及其轨道。使用HF优化的单电子的分子轨道，φ_μ(r)随后被用作PauliNet输入，并在训练期间由且仅由backflow transformation修改。

当电子彼此接近并且原子核接近时，任何基态电子波函数都遵循由尖峰条件定义的精确渐近行为。作者选择将尖峰条件直接构建到PauliNet函数形式中，因为这样可以消除局部电子能量的差异，从而使训练更加高效稳定。

稳健的深度Jastrow factor和backflow

PauliNet与常规QMC拟设的不同之处在于：它使用DNN来表示Jastrow factor和backflow 函数。为了保留波函数的反对称性，用以计算Jastro factor和backflow的DNN在设计之初即分别具有针对相同自旋电子交换（mathcal{P}_ij）的不变性和等变性。

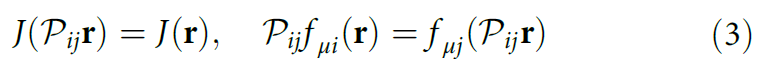
作者发现尝试用DNN表示耦合电子坐标的标准backflow形式会导致优化比较困难。因此，PauliNet的backflow的形式是将裸露的单电子分子轨道与多电子等变函数f（方程（1））相乘。结合少数几个行列式，就可以很好地表示电子节点表面。另外，构建用以学习势能函数的DNN与以下两者密切相关：粒子排列的不变性和等变性、以及粒子相互作用是其距离的函数。最终，PauliNet使用了一种这样的DNN架构——SchNet——的修改版本。

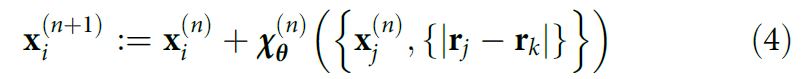
用更少的行列式得到更精确的结果

作者通过变分原理训练PauliNet，使总电子能最小化（变异QMC）。通过采样电子分布|ψ|^2，在运行时生成的电子构型作为训练数据。我们首先测试了在DeepWF中使用过的测试体系，特别是氢分子（H_2）、氢化锂（LiH）、铍（Be）、硼（B）和线性氢链H_10。在单个GTX 1080 Ti图形处理单元(GPU)上训练几十分钟到几小时后，对于单原子和双原子体系PauliNet可以准确计算97%到99.9%的电子相关能量（图3），在所有情况下都远超DeepWF的精度。作者将这些结果与标准的单行列式和多行列式、包括或不包括backflow的变分蒙特卡洛（VMC）方法进行比较。在所有情况下，使用6个行列式的PauliNet都比单行列式和少数行列式的的拟设表现更好，并且仅被具有数十或数百个构型状态函数（CSF）的波函数所超越，而这些相当于数百到数千行列式。

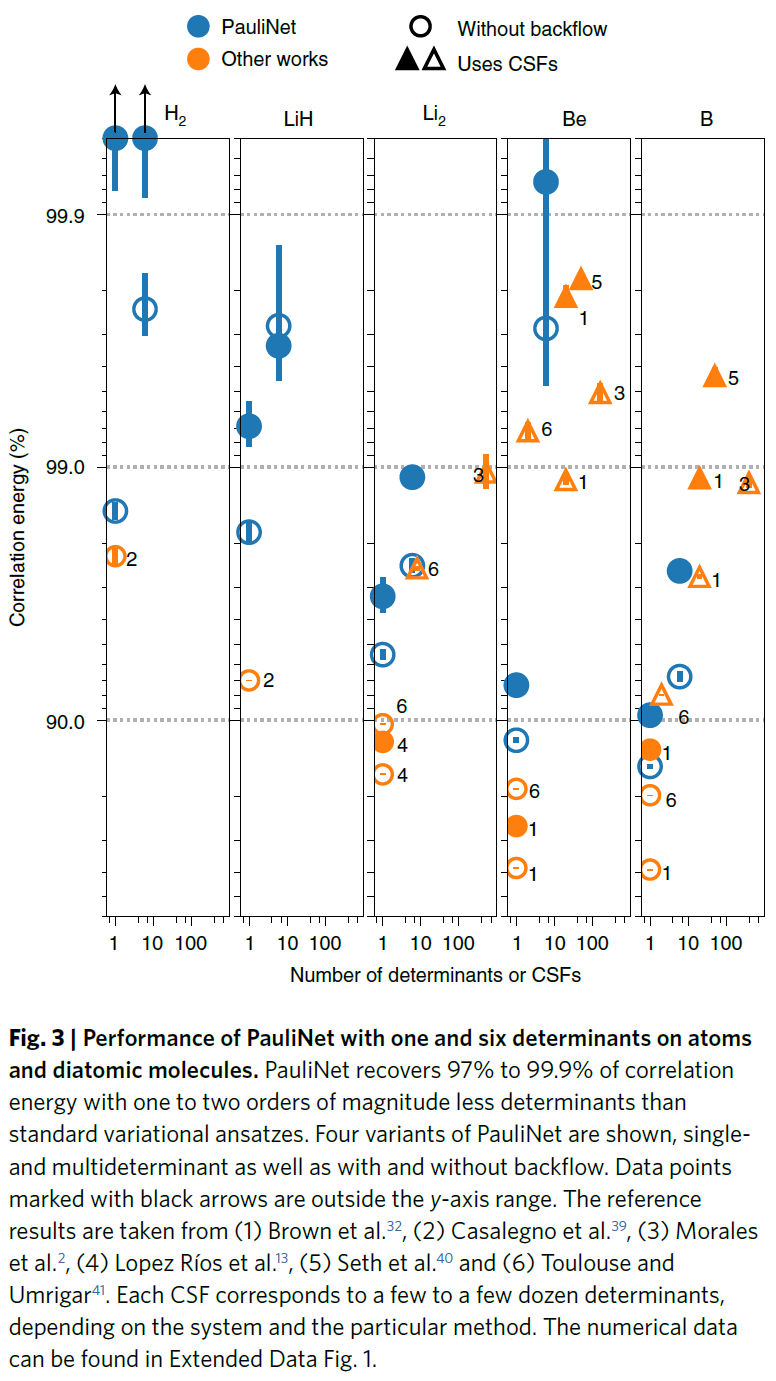
图3 PauliNet的性能

数据来源：Nature Chemistry

图4强调了作者方法的两个关键方面。首先，随着训练从最初的HF基线水平发展到最终报告的值，相关能量的误差单调减少。在大多数情况下，学习曲线还没有完全稳定下来，这表明了PauliNet具有很强的表示能力，并表明使用更多的计算资源可以实现更高的准确性。其次，作者将完整的拟设与仅使用单个行列式的变体、与没有backflow的变体分别进行了比较，发现这两个组件对于优化HF基线的节点表面并因此达到较高的准确性非常重要。通过强大的backflow transformation，增加的每个行列式都大大增加了拟设的灵活性。

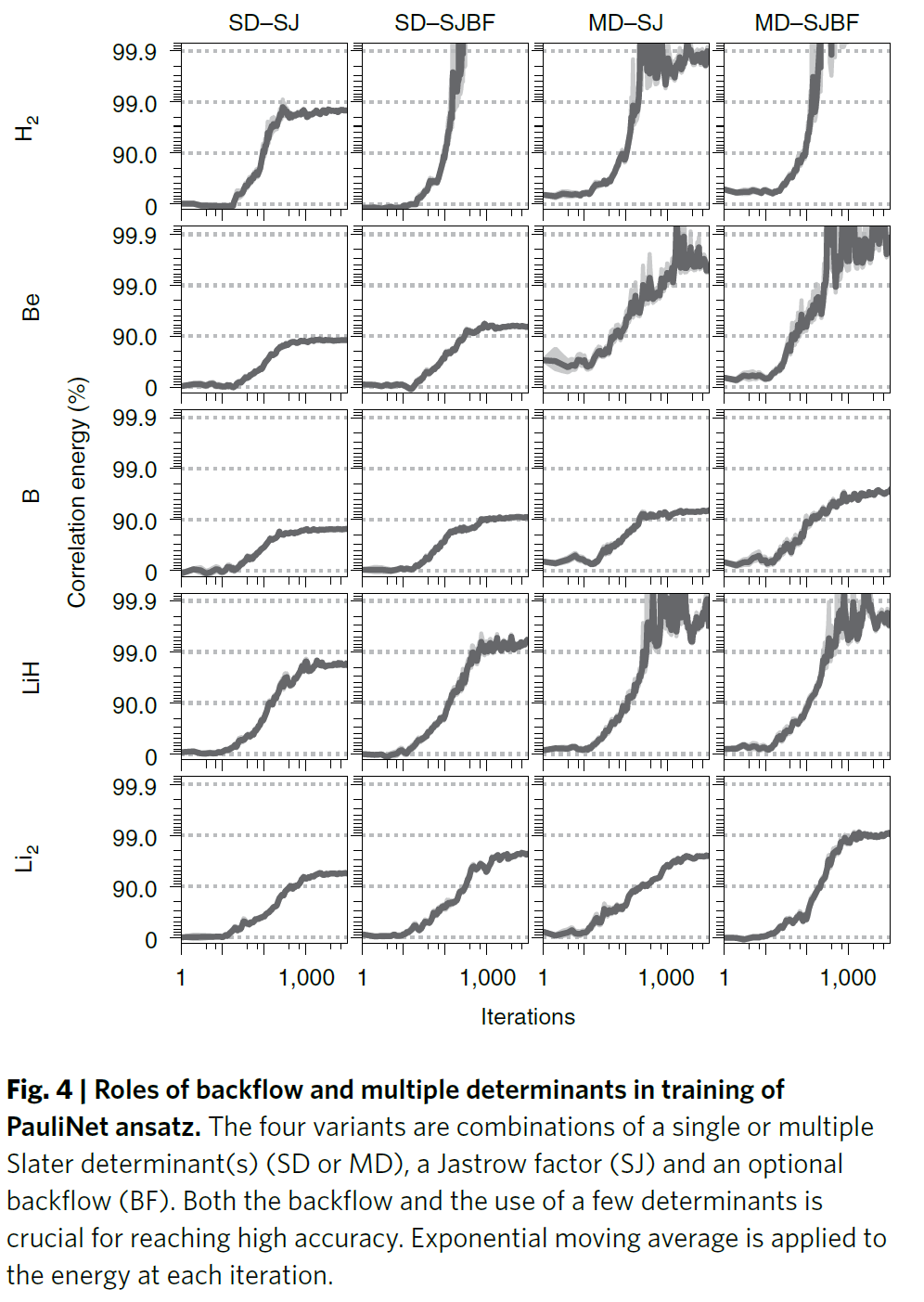
图4 backflow和多行列式在PauliNet训练中的作用

数据来源：Nature Chemistry

作者进一步分析了按比例增加行列式数目和体系大小时PauliNet的表现。在四种同元素双原子分子（Li_2到C_2）中，PauliNet均可以以较少的行列式得到高准确度的结果。在几到几十个行列式范围内，PauliNet超过了现有的变分方法结果；甚至在大多数情况下，达到了相应扩散蒙特卡罗（DMC）结果的准确性。作者注意到，使用PauliNet实现DMC并不困难，而这有望进一步提高其准确性。 

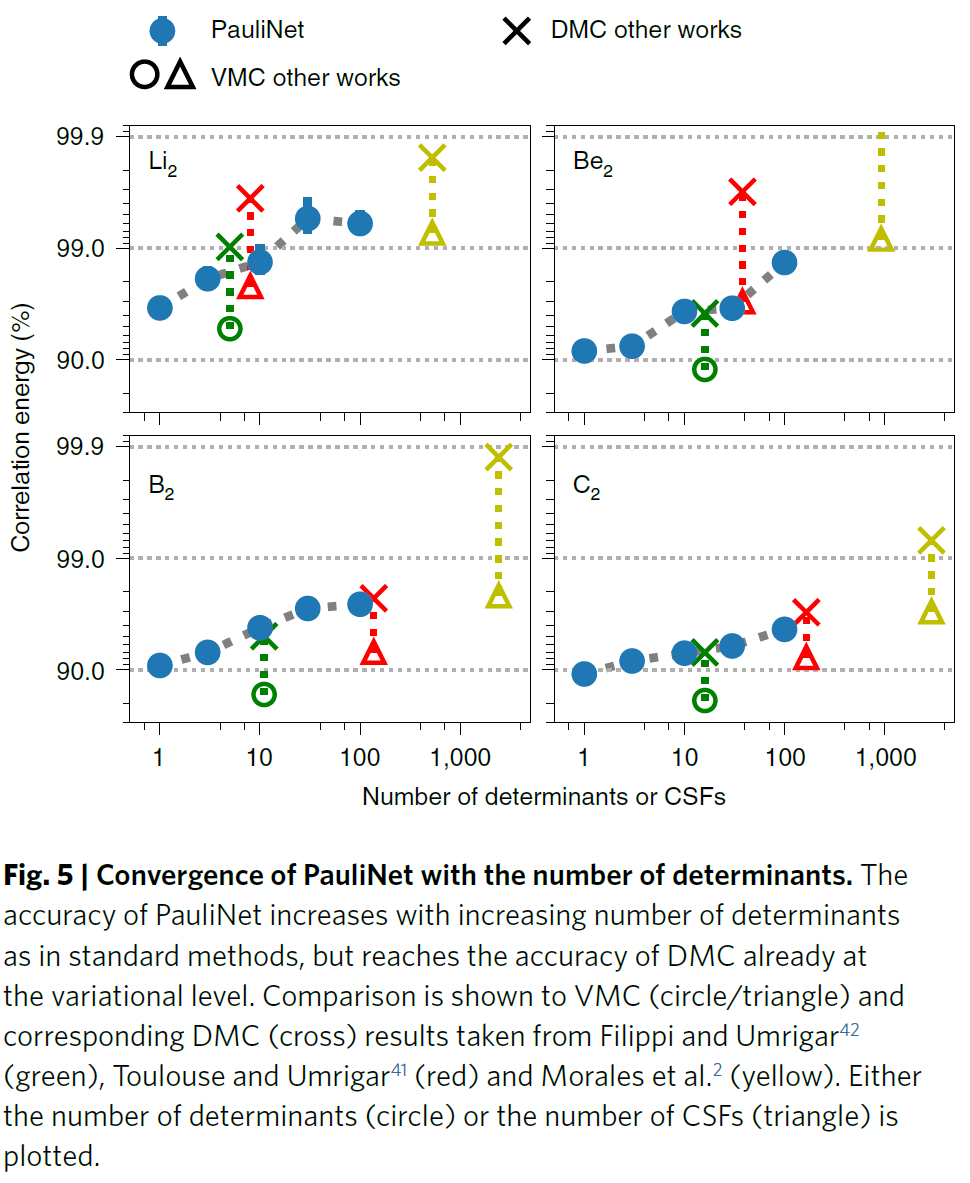
图5 PauliNet准确度与行列式数量

数据来源：Nature Chemistry

捕获强相关能

与原子和双原子不同，线性氢链H_10显示出很强的相关性，相关能占电子能量的重要部分而单行列式或少数行列式的HF方法无法描述这类体系。

对于H_10的平衡构象和拉伸构象，PauliNet使用16个行列式可分别计算出98.41(8)％和98.4(3)％的相关能（图6）。使用一个单独的行列式（98.10(9)％和97.5(4)％），结果只会稍差一些，但是当同时移除backflow时（93.7(2)％和82(2)％），结果则明显变差。与标准的VMC拟设相比，PauliNet效果更好。

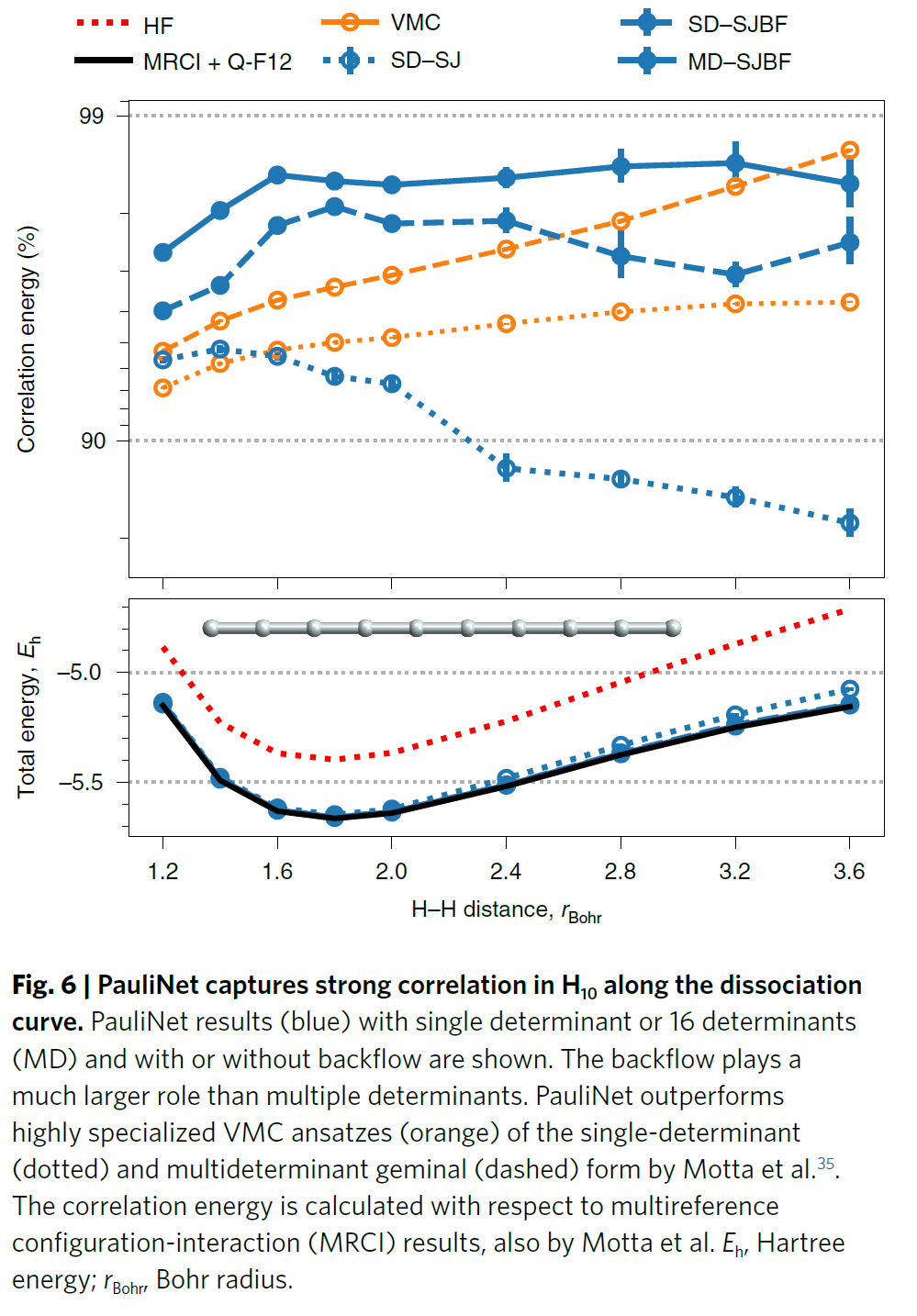
图6 PauliNet与H_10 

数据来源：Nature Chemistry

应用到更大的体系上

前面两节展示了PauliNet在相对较小的基准体系上的性能，对于这些体系，已经可以从成熟的方法中得到基本准确的结果。在本节中，作者直接将PauliNet用于具有复杂电子结构的大分子上，对于这些分子，只有高度定制化量子化学方法才能提供令人满意的结果。作者选择了环丁二烯的互变异构化（图7a，28个电子），这一化学过程同时受到了实验化学和理论化学的极大关注。实验估计势垒范围在1.6到10 kcal/mol之间，而CCSD(T)方法预测结构为18 kcal/mol，高估了2倍左右。从MR-CC方法中得到的结果是目前最好的，为7到11 kcal/mol之间。

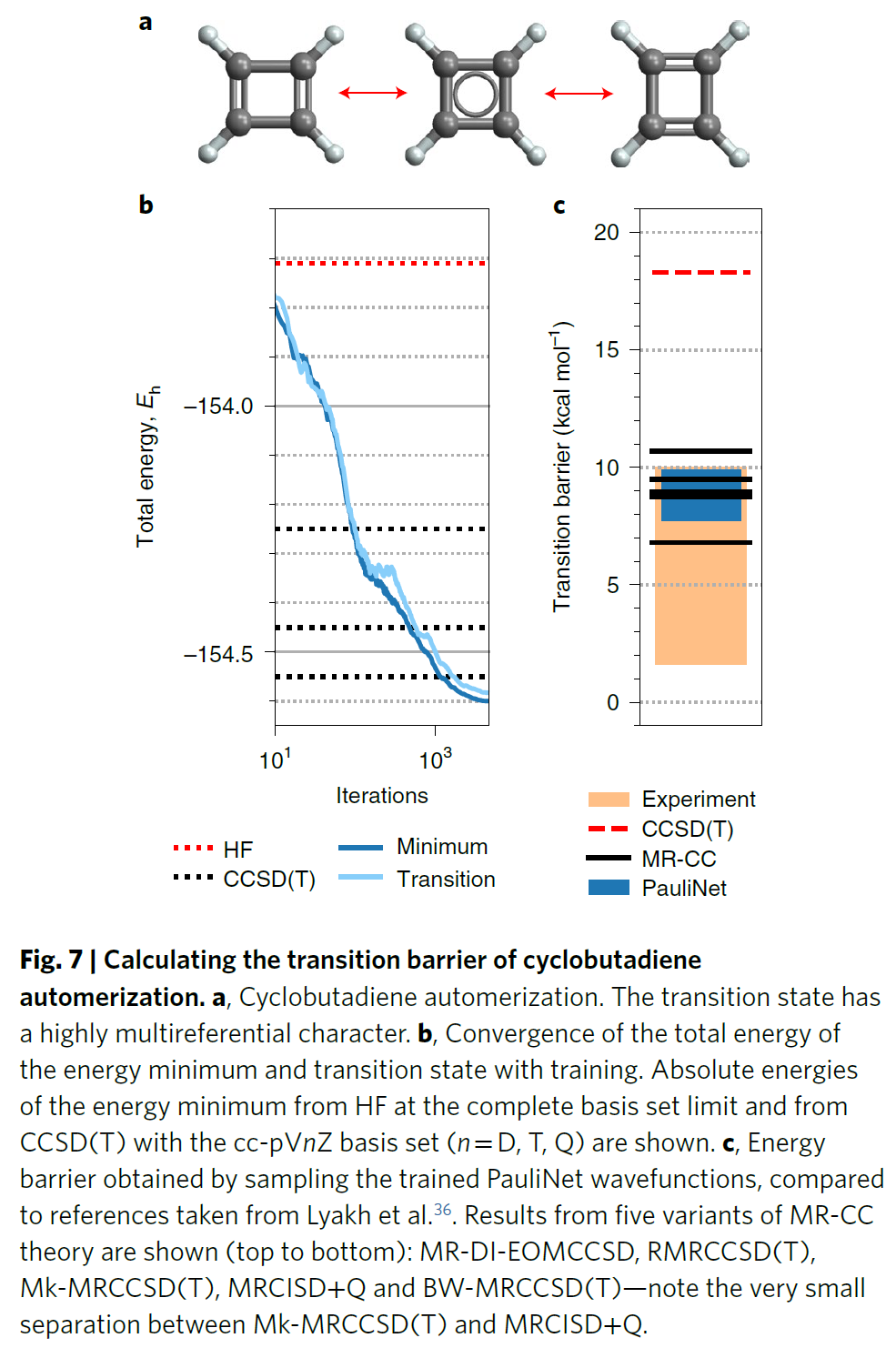
图7计算环丁二烯互变异构化的势垒

数据来源：Nature Chemistry

使用PauliNet 和10个行列式和与此前小体系上相同的超参数，作者获得了环丁二烯的最小能级和过渡态的全电子变分能量，从而获得了势垒。由于能量屏障仅占总能量的0.01％，因此作者使用改进的优化协议来稳定神经网络的训练。通过此修改，总能量平稳收敛（图7b）。通过以250和375次迭代的同步周期运行两个独立的优化，作者获得了分别为9.9±0.6和7.7±0.6 kcal/mol的能垒估计值，两个结果都在MR-CC方法预测值所覆盖的范围内。作者提到，与需要使用特定于系统和状态的波函数拟设的MR-CC方法相比，PauliNet拟设可以对所有体系使用同一套参数。对于环丁二烯的每个同步优化，在单个GTX 1080 Ti GPU上每次迭代需要50s。

讨论

PauliNet，作为一个实数空间中电子波函数的DNN表示，效果优于不使用大量行列式扩展的最先进的变分量子化学方法。因此，PauliNet可以高精度地扩展到更大的体系。

与QMC中使用的标准函数形式相比，使用DNN有几个优点。首先，DNN更高的灵活性使得变分方法可以达到或超过DMC的精度，这有助于精确计算出包括电子能在内的各种电子性质。第二，除了编码电子间更复杂的多体相关性外，DNN在空间自由度上的灵活性基本不受限制，规避了量子化学不完全基组的“诅咒”。第三，标准QMC中接近重核的局部能量的快速振荡，使得过渡金属等较重元素必须使用伪势。DNN的灵活性可以通过平滑这种振荡来避开这种必要性。

在经典量子化学方法中，强相关性通常是通过使用大量的多行列式扩展来处理的，这对计算要求很高，并引入了如何选择适当的行列式的问题。作者表明，DNN能够学习电子之间的强相关性，而不需要任何专门的调整。虽然目前还不清楚这在严格的数学意义上是否具有优势，但这恰恰是DNN在各种现实世界应用中被证明为强项的任务。

简单的对比了PauliNet与FermiNet可以发现两种架构潜在的改进方向。将在FermiNet的架构设计和优化方法与PauliNet的物理约束相结合，用于发展一种计算上负担得起的、可扩展的、且高度精确的量子化学黑盒方法，似乎是一个很有希望的方向。

参考文献

Hermann, J., Schätzle, Z. & Noé, F. Deep-neural-network solution of the electronic Schrödinger equation. Nat. Chem. 12, 891–897 (2020).